Fast Normalized Cross-Correlation

J. P. Lewis¹
Industrial Light & Magic

Abstract:

Although it is well known that cross correlation can be efficiently implemented in the transform domain, the normalized form of cross correlation preferred for feature matching applications does not have a simple frequency domain expression. Normalized cross correlation has been computed in the spatial domain for this reason. This short paper shows that unnormalized cross correlation can be efficiently normalized using precomputing integrals of the image and image² over the search window.

Introduction

The correlation between two signals (cross correlation) is a standard approach to feature detection [6,7] as well as a component of more sophisticated techniques (e.g. [3]). Textbook presentations of correlation describe the convolution theorem and the attendant possibility of efficiently computing correlation in the frequency domain using the fast Fourier transform. Unfortunately the normalized form of correlation (correlation coefficient) preferred in template matching does not have a correspondingly simple and efficient frequency domain expression. For this reason normalized cross-correlation has been computed in the spatial domain (e.g., [7], p. 585). Due to the computational cost of spatial domain convolution, several inexact but fast spatial domain matching methods have also been developed [2]. This paper describes a recently introduced algorithm [10] for obtaining normalized cross correlation from transform domain convolution. The new algorithm in some cases provides an order of magnitude speedup over spatial domain computation of normalized cross correlation (Section 5).

Since we are presenting a version of a familiar and widely used algorithm no attempt will be made to survey the literature on selection of features, whitening, fast convolution techniques, extensions, alternate techniques, or applications. The literature on these topics can be approached through introductory texts and handbooks [16,7,13] and recent papers such as [1,19]. Nevertheless, due to the variety of feature tracking schemes that have been advocated it may be necessary to establish that normalized cross-correlation remains a viable choice for some if not all applications. This is done in section 3.

In order to make the paper self contained, section 2 describes normalized cross-correlation and section 4 briefly reviews transform domain and other fast convolution approaches and the phase correlation technique. These sections can be skipped by most readers. Section 5 describes how normalized cross-correlation can be obtained from a transform domain computation of correlation. Section 6 presents performance results.

Template Matching by Cross-Correlation

The use of cross-correlation for template matching is motivated by the distance measure (squared Euclidean distance)

$$d^2_{f,t}(u,v) = \sum_{x,y}[f(x,y) -t( x-u,y-v)]^2$$

(where f is the image and the sum is over x,y under the window containing the feature t positioned at u,v). In the expansion of d²

$$\begin{eqnarray*}d^2_{f,t}(u,v) = \sum_{x,y}[f^2(x,y) & - & 2f(x,y)t(x-u,y-v) \\ & + & t^2(x-u,y-v)] \end{eqnarray*}$$

the term $\sum t^2(x-u,y-v)$ is constant. If the term $\sum f^2(x,y)$ is approximately constant then the remaining cross-correlation term

$$c(u,v) = \sum_{x,y}f(x,y)t(x-u,y-v)$$ (1)

is a measure of the similarity between the image and the feature.

There are several disadvantages to using (1) for template matching:

• If the image energy $\sum f^2(x,y)$ varies with position, matching using (1) can fail. For example, the correlation between the feature and an exactly matching region in the image may be less than the correlation between the feature and a bright spot.
• The range of c(u,v) is dependent on the size of the feature.
• Eq. (1) is not invariant to changes in image amplitude such as those caused by changing lighting conditions across the image sequence.

The correlation coefficient overcomes these difficulties by normalizing the image and feature vectors to unit length, yielding a cosine-like correlation coefficient

$$\gamma(u, v) = \hspace{.8\columnwidth minus .8\columnwidth}$$ (2)

$$\frac{ \sum_{x,y} [ f(x,y) - \bar{f}_{u,v} ] [t(x-u, y-v) - \... ...] ^2 \sum_{x,y} [t(x-u, y-v) - \bar{t} ] ^2 \right\} ^{0.5} }$$

where $\bar{t}$ is the mean of the feature and $\bar{f}_{u,v}$ is the mean of f(x,y) in the region under the feature. We refer to (2) as normalized cross-correlation.

Feature Tracking Approaches and Issues

It is clear that normalized cross-correlation (NCC) is not the ideal approach to feature tracking since it is not invariant with respect to imaging scale, rotation, and perspective distortions. These limitations have been addressed in various schemes including some that incorporate NCC as a component. This paper does not advocate the choice of NCC over alternate approaches. Rather, the following discussion will point out some of the issues involved in various approaches to feature tracking, and will conclude that NCC is a reasonable choice for some applications.

SSDA. The basis of the sequential similarity detection algorithm (SSDA) [2] is the observation that full precision is only needed near the maximum of the cross-correlation function, while reduced precision can be used elsewhere. The authors of [2] describe several ways of implementing `reduced precision'. An SSDA implementation of cross-correlation proceeds by computing the summation in (1) in random order and uses the partial computation as a Monte Carlo estimate of whether the particular match location will be near a maximum of the correlation surface. The computation at a particular location is terminated before completing the sum if the estimate suggests that the location corresponds to a poor match.

The SSDA algorithm is simple and provides a significant speedup over spatial domain cross-correlation. It has the disadvantage that it does not guarantee finding the maximum of the correlation surface. SSDA performs well when the correlation surface has shallow slopes and broad maxima. While this condition is probably satisfied in many applications, it is evident that images containing arrays of objects (pebbles, bricks, other textures) can generate multiple narrow extrema in the correlation surface and thus mislead an SSDA approach. A secondary disadvantage of SSDA is that it has parameters that need to determined (the number of terms used to form an estimate of the correlation coefficient, and the early termination threshold on this estimate).

Gradient Descent Search. If it is assumed that feature translation between adjacent frames is small then the translation (and parameters of an affine warp in [19]) can be obtained by gradient descent [12]. Successful gradient descent search requires that the interframe translation be less than the radius of the basin surrounding the minimum of the matching error surface. This condition may be satisfied in many applications. Images sequences from hand-held cameras can violate this requirement, however: small rotations of the camera can cause large object translations. Small or (as with SSDA) textured templates result in matching error surfaces with narrow extrema and thus constrain the range of interframe translation that can be successfully tracked. Another drawback of gradient descent techniques is that the search is inherently serial, whereas NCC permits parallel implementation.

Snakes. Snakes (active contour models) have the disadvantage that they cannot track objects that do not have a definable contour. Some ``objects'' do not have a clearly defined boundary (whether due to intrinsic fuzzyness or due to lighting conditions), but nevertheless have a characteristic distribution of color that may be trackable via cross-correlation. Active contour models address a more general problem than that of simple template matching in that they provide a representation of the deformed contour over time. Cross-correlation can track objects that deform over time, but with obvious and significant qualifications that will not be discussed here. Cross-correlation can also easily track a feature that moves by a significant fraction of its own size across frames, whereas this amount of translation could put a snake outside of its basin of convergence.

Wavelets and other multi-resolution schemes. Although the existence of a useful convolution theorem for wavelets is still a matter of discussion (e.g., [11]; in some schemes wavelet convolution is in fact implemented using the Fourier convolution theorem), efficient feature tracking can be implemented with wavelets and other multi-resolution representations using a coarse-to-fine multi-resolution search. Multi-resolution techniques require, however, that the images contain sufficient low frequency information to guide the initial stages of the search. As discussed in section 6, ideal features are sometimes unavailable and one must resort to poorly defined ``features'' that may have little low-frequency information, such as a configuration of small spots on an otherwise uniform surface.

Each of the approaches discussed above has been advocated by various authors, but there are fewer comparisons between approaches. Reference [19] derives an optimal feature tracking scheme within the gradient search framework, but the limitations of this framework are not addressed. An empirical study of five template matching algorithms in the presence of various image distortions [4] found that NCC provides the best performance in all image categories, although one of the cheaper algorithms performs nearly as well for some types of distortion. A general hierarchical framework for motion tracking is discussed in [1]. A correlation based matching approach is selected though gradient approaches are also considered.

Despite the age of the NCC algorithm and the existence of more recent techniques that address its various shortcomings, it is probably fair to say that a suitable replacement has not been universally recognized. NCC makes few requirements on the image sequence and has no parameters to be searched by the user. NCC can be used `as is' to provide simple feature tracking, or it can be used as a component of a more sophisticated (possibly multi-resolution) matching scheme that may address scale and rotation invariance, feature updating, and other issues. The choice of the correlation coefficient over alternative matching criteria such as the sum of absolute differences has also been justified as maximum-likelihood estimation [18]. We acknowledge NCC as a default choice in many applications where feature tracking is not in itself a subject of study, as well as an occasional building block in vision and pattern recognition research (e.g. [3]). A fast algorithm is therefore of interest.

Transform Domain Computation

Consider the numerator in (2) and assume that we have images $f'(x,y) \equiv f(x,y) - \bar{f}_{u,v}$ and $t'(x,y) \equiv t(x,y) - \bar{t}$ in which the mean value has already been removed:

$$\stackrel{\rm num}{\gamma}(u,v) = \sum_{x,y} f'(x,y)t'(x-u,y-v)$$ (3)

For a search window of size M² and a feature of size N² (3) requires approximately N² ( M - N + 1)² additions and N² ( M - N + 1)² multiplications.

Eq. (3) is a convolution of the image with the reversed feature t'(-x,-y) and can be computed by

$${\cal{F}} ^{-1}\{ {\cal{F}} (f') {\cal{F}} ^*(t')\}$$ (4)

where ${\cal{F}}$ is the Fourier transform. The complex conjugate accomplishes reversal of the feature via the Fourier transform property ${\cal{F}} f^{\ast}(-x) = F^{\ast}(\omega)$.

Implementations of the FFT algorithm generally require that f' and t' be extended with zeros to a common power of two. The complexity of the transform computation (3) is then 12 M² log₂ M real multiplications and 18 M² log₂ M real additions/subtractions. When M is much larger than N the complexity of the direct `spatial' computation (3) is approximately N²M² multiplications/additions, and the direct method is faster than the transform method. The transform method becomes relatively more efficient as N approaches M and with larger M, N.

Fast Convolution

There are several well known ``fast'' convolution algorithms that do not use transform domain computation [13]. These approaches fall into two categories: algorithms that trade multiplications for additional additions, and approaches that find a lower point on the O(N²) characteristic of (one-dimensional) convolution by embedding sections of a one-dimensional convolution into separate dimensions of a smaller multidimensional convolution. While faster than direct convolution these algorithms are nevertheless slower than transform domain convolution at moderate sizes [13] and in any case they do not address computation of the denominator of (2).

Phase Correlation

Because (4) can be efficiently computed in the transform domain, several transform domain methods of approximating the image energy normalization in (2) have been developed. Variation in the image energy under the template can be reduced by high-pass filtering the image before cross-correlation. This filtering can be conveniently added to the frequency domain processing, but selection of the cutoff frequency is problematic--a low cutoff may leave significant image energy variations, whereas a high cutoff may remove information useful to the match.

A more robust approach is phase correlation [9]. In this approach the transform coefficients are normalized to unit magnitude prior to computing correlation in the frequency domain. Thus, the correlation is based only on phase information and is insensitive to changes in image intensity. Although experience has shown this approach to be successful, it has the drawback that all transform components are weighted equally, whereas one might expect that insignificant components should be given less weight. In principle one should select the spectral pre-filtering so as to maximize the expected correlation signal-to-noise ratio given the expected second order moments of the signal and signal noise. This approach is discussed in [16] and is similar to the classical matched filtering random signal processing technique. With typical ( $\rho \approx 0.95$) image correlation the best pre-filtering is approximately Laplacian rather than a pure whitening.

Normalizing

Examining again the numerator of (2), we note that the mean of the feature can be precomputed, leaving

$$\begin{eqnarray*}\stackrel{\rm num}{\gamma} (u, v) & = & \sum f(x,y)t'(x-u,y-v) \\ & - & \bar{f}_{u,v} \sum t'(x-u,y-v) \end{eqnarray*}$$

Since t' has zero mean and thus zero sum the term $\bar{f}_{u,v} \sum t'(x-u,y-v)$ is also zero, so the numerator of the normalized cross-correlation can be computed using (4).

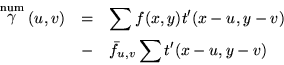
Examining the denominator of (2), the length of the feature vector can be precomputed in approximately 3N² operations (small compared to the cost of the cross-correlation), and in fact the feature can be pre-normalized to length one.

The problematic quantities are those in the expression $\sum_{x,y} [ f(x,y) - \bar{f}_{u,v} ] ^2$. The image mean and local (RMS) energy must be computed at each u,v, i.e. at (M-N+1)² locations, resulting in almost 3N²(M-N+1)² operations (counting add, subtract, multiply as one operation each). This computation is more than is required for the direct computation of (3) and it may considerably outweight the computation indicated by (4) when the transform method is applicable. A more efficient means of computing the image mean and energy under the feature is desired.

These quantities can be efficiently computed from tables containing the integral (running sum) of the image and image square over the search area, i.e.,

s(u,v) = f(u,v) + s(u-1,v) + s(u,v-1) - s(u-1,v-1)

$$\begin{eqnarray*}s^2(u,v) = f^2(u,v) &+& s^2(u-1,v) \\ &+& s^2(u,v-1) - s^2(u-1,v-1) \end{eqnarray*}$$

with s(u,v) = s²(u,v) = 0 when either u,v < 0. The energy of the image under the feature positioned at u,v is then

$$\begin{eqnarray*}e_f(u,v) = & s^2(u+N-1,v+N-1) \\ - & s^2(u-1,v+N-1) \\ - & s^2(u+N-1,v-1) \\ + & s^2(u-1,v-1) \end{eqnarray*}$$

and similarly for the image sum under the feature.

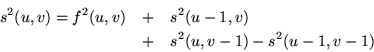
The problematic quantity $\sum_{x,y} [ f(x,y) - \bar{f}_{u,v} ] ^2$ can now be computed with very few operations since it expands into an expression involving only the image sum and sum squared under the feature. The construction of the tables requires approximately 3M² operations, which is less than the cost of computing the numerator by (4) and considerably less than the 3N²(M-N+1)² required to compute $\sum_{x,y} [ f(x,y) - \bar{f}_{u,v} ] ^2$ at each u,v.

This technique of computing a definite sum from a precomputed running sum has been independently used in a number of fields; a computer graphics application is developed in [5]. If the search for the maximum of the correlation surface is done in a systematic row-scan order it is possible to combine the table construction and reference through state variables and so avoid explicitly storing the table. When implemented on a general purpose computer the size of the table is not a major consideration, however, and flexibility in searching the correlation surface can be advantageous. Note that the s(u,v) and s²(u,v) expressions are marginally stable, meaning that their z-transform H(z) = 1/(1 - z^-1) (one dimensional version here) has a pole at z=1, whereas stability requires poles to be strictly inside the unit circle [14]. The computation should thus use large integer rather than floating point arithmetic.

 

Figure 1: Measured relative performance of transform domain versus spatial domain normalized cross-correlation as a function of the search window size (depth axis) and the ratio of the feature size to search window size.

Table: Two tracking sequences from Forest Gump were re-timed using both direct and fast NCC algorithms using identical features and search windows on a 100 Mhz R4000 processor. These times include a 16² sub-pixel search [17] at the location of the best whole-pixel match. The sub-pixel search was computed using Eq. (2) (direct convolution) in all cases.

search window(s)	length	direct NCC	fast NCC
$168 \times 86$	896 frames	15 hours	1.7 hours
$115 \times 200,150 \times 150$	490 frames	14.3 hours	57 minutes

feature size	search window(s)	Flint	fast NCC
402	1102	1 min. 40 seconds	16 seconds (subpixel=1)
402	1102	n/a	21 seconds (subpixel=8)

Performance

 

Figure 2: A tracked feature from a special effects sequence in the movie Forest Gump. The region is out of focus and has noticeable film-grain noise across frames. A small (e.g. 10² or smaller) area from this region would not provide a usable feature. The chosen feature size is more than 40² pixels.

The performance of this algorithm will be discussed in the context of special effects image processing. The integration of synthetic and processed images into special effects sequences often requires accurate tracking of sequence movement and features. The use of automated feature tracking in special effects was pioneered in movies such as Cliffhanger, Forest Gump, and Speed. Recently cross-correlation based feature trackers have been introduced in commercial image compositing systems such as Flame/Flint [20], Matador, Advance [21], and After Effects [22].

The algorithm described in this paper was developed for the movie Forest Gump (1994), and has been used in a number of subsequent projects. Special effects sequences in that movie included the replacement of various moving elements and the addition of a contemporary actor into historical film and video sequences. Manually picked features from one frame of a sequence were automatically tracked over the remaining frames; this information was used as the basis for further processing.

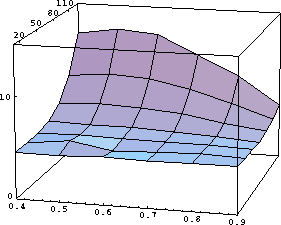
The relative performance of our algorithm is a function of both the search window size and the ratio of the feature size to search window size. Relative performance increases along the window size axis (Fig. 1); a higher resolution plot would show an additional ripple reflecting the relation between the search window size and the bounding power of two. The property that the relative performance is greater on larger problems is desirable. Table 1 illustrates the performance obtained in a special effects feature tracking application. Table 2 compares the performance of our algorithm with that of a high-end commercial image compositing package.

Note that while a small (e.g. 10²) feature size would suffice in an ideal digital image, in practice much larger feature sizes and search windows are sometimes required or preferred:

• The image sequences used in film and video are sometimes obtained from moving cameras and may have considerable translation between frames due to camera shake. Due to the high resolution required to represent digital film, even a small movement across frames may correspond to a distance of many pixels.
• The selected features are of course constrained to the available features in the image; distinct ``features'' are not always available at preferred scales and locations.
• Many potential features in a typical digitized image are either out of focus or blurred due to motion of the camera or object (Fig. 2). Feature match is also hindered by imaging noise such as film grain. Large features are more accurate in the presence of blur and noise.

As a result of these considerations feature sizes of 20² and larger and search windows of 50² and larger are often employed.

The fast algorithm in some cases reduces high-resolution feature tracking from an overnight to an over-lunch procedure. With lower (``proxy'') resolution and faster machines, semi-automated feature tracking is tolerable in an interactive system. Certain applications in other fields may also benefit from the algorithm described here.²

Bibliography

1

P. Anandan, ``A Computational Framework and an Algorithm for the Measurement of Visual Motion'', Int. J. Computer Vision, 2(3), p. 283-310, 1989.

2

D. I. Barnea, H. F. Silverman, ``A class of algorithms for fast digital image registration'', IEEE Trans. Computers, 21, pp. 179-186, 1972.

3

R. Brunelli and T. Poggio, ``Face Recognition: Features versus Templates", IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 15, no. 10, pp. 1042-1052, 1993.

4

P. J. Burt, C. Yen, X. Xu, ``Local Correlation Measures for Motion Analysis: a Comparitive Study'', IEEE Conf. Pattern Recognition Image Processing 1982, pp. 269-274.

5

F. Crow, ``Summed-Area Tables for Texture Mapping'', Computer Graphics, vol 18, No. 3, pp. 207-212, 1984.

6

R. O. Duda and P. E. Hart, Pattern Classification and Scene Analysis, New York: Wiley, 1973.

7

R. C. Gonzalez and R. E. Woods, Digital Image Processing (third edition), Reading, Massachusetts: Addison-Wesley, 1992.

8

A. Goshtasby, S. H. Gage, and J. F. Bartholic, ``A Two-Stage Cross-Correlation Approach to Template Matching'', IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 6, no. 3, pp. 374-378, 1984.

9

C. Kuglin and D. Hines, ``The Phase Correlation Image Alignment Method,'' Proc. Int. Conf. Cybernetics and Society, 1975, pp. 163-165.

10

J. P. Lewis, ``Fast Template Matching'', Vision Interface, p. 120-123, 1995.

11

A. R. Lindsey, ``The Non-Existence of a Wavelet Function Admitting a Wavelet Transform Convolution Theorem of the Fourier Type'', Rome Laboratory Technical Report C3BB, 1995.

12

B. D. Lucas and T. Kanade, ``An Iterative Image Registration Technique with an Application to Stereo Vision'', IJCAI 1981.

13

S. K. Mitra and J. F. Kaiser, Handbook for Digital Signal Processing, New York: Wiley, 1993.

14

A. V. Oppenheim and R. W. Schafer, Digital Signal Processing, Englewood Cliffs, New Jersey: Prentice-Hall, 1975.

15

D. Polk, ``Product Probe'' - Panasonic PV-IQ604, Videomaker, October 1994, pp. 55-57.

16

W. Pratt, Digital Image Processing, John Wiley, New York, 1978.

17

Qi Tian and M. N. Huhns, ``Algorithms for Subpixel Registration'', CVGIP 35, p. 220-233, 1986.

18

T. W. Ryan, ``The Prediction of Cross-Correlation Accuracy in Digital Stereo-Pair Images'', PhD thesis, University of Arizona, 1981.

19

J. Shi and C. Tomasi, ``Good Features to Track'', Proc. IEEE Conf. on Computer Vision and Pattern Recognition, 1994.

20

Flame effects compositing software, Discreet Logic, Montreal, Quebec.

21

Advance effects compositing software, Avid Technology, Inc., Tewksbury, Massachusetts.

22

After Effects effects compositing software, Adobe (COSA), Mountain View, California.

Footnotes

... Lewis¹

Current address: Interval Research, Palo Alto CA zilla@computer.org

... here.²

For example, image stabilization is a common feature in recent consumer video cameras. Although most such systems are stabilized by inertial means, one manufacturer implemented digital stabilization and thus presumably used some form of image tracking. The algorithm used leaves room for improvement however: it has been criticized as being slow and unpredictable and a product review recommended leaving it disabled [15].