| |
(1) |
J. P. Lewis1
Computer Graphics Laboratory
New York Institute of Technology
Stochastic techniques have assumed a prominent role in computer graphics, because of their success in modeling a variety of complex and natural phenomena. This paper describes the basis for techniques such as stochastic subdivision in the theory of random processes and estimation theory. The popular stochastic subdivision construction is then generalized to provide control of the autocorrelation and spectral properties of the synthesized random functions. The generalized construction is suitable for generating a variety of perceptually distinct high-quality random functions, including those with non-fractal spectra and directional or oscillatory characteristics. It is argued that a spectral modeling approach provides a more powerful and somewhat more intuitive perceptual characterization of random processes than does the fractal model. Synthetic textures and terrains are presented as a means of visually evaluating the generalized subdivision technique.
Categories and Subject Descriptors: I.3.3 [Computer Graphics]: Picture/Image Generation; I.3.7 [Computer Graphics]: Three Dimensional Graphics and Realism - color, shading, shadowing and texture.
General Terms: Algorithms, Theory
Additional Keywords and Phrases: Fractals, modeling of natural phenomena, stochastic interpolation, stochastic models, texture synthesis
The application of stochastic models in the computer graphic synthesis of complex phenomena has been termed amplification [40]. The image modeler specifies characteristic structural or statistical features and other constraints in the form of a pseudo-random procedure and its parameters. The procedure can then automatically generate the vast amount of detail necessary to create a naturalistic or organic model, in a sense ``amplifying'' the information directly specified by the modeler. In addition, a versatile stochastic model that may be adjusted to approximately emulate a range of different phenomena reduces the need to develop procedures to model each of these phenomena individually. For these reasons, stochastic techniques have assumed a leading role in the synthesis of complex images (e.g., [10,35,36,43,31]).
The usefulness of a particular stochastic model depends on both its computational advantages and on the extent to which it can be adjusted to describe different phenomena. The stochastic fractal techniques are somewhat limited in descriptive power in that they model only power spectra of the form f - d of a single parameter d and hence cannot differentiate more structured phenomena, for example, those with directional or oscillatory characteristics. The fractal subdivision construction described by Fournier, Fussell, and Carpenter [10,4], however, has several properties that make it very attractive for the purpose of producing perspective and animated renderings of stochastic models:
In this paper we generalize the stochastic subdivision construction [10] to produce random functions with prescribed correlations and spectra. The generalized subdivision technique produces high-quality random functions (Figure 4) while preserving most of the computational advantage of the subdivision approach. In addition, this technique appears to provide both reasonably intuitive and general control over the appearance of the random function.
There is a considerable literature on the theory and application of stochastic models in all fields, although much of it deals with problems (such as discrimination or particular parameter estimates) that are not closely related to our purpose of synthesizing random functions. This section will briefly review some of the relevant terminology and definitions from random processes [45], with emphasis on the restrictions and scope of a computationally realizable stochastic synthesis model.
A random process is statistically characterized by its
joint nth-order distribution functions F x.
For a one-dimensional process these statistics are
A stochastic process is called stationary or homogeneous if all the joint probability distribution functions are invariant with respect to a translation of the time or space origin. A random field is isotropic if its statistics are also invariant to rotation of the coordinate system. A random process is ergodic if its statistics are identical for all realizations of the process. A nonergodic process is often one in which random initial conditions significantly affect the subsequent character of the process. The ergodic property is important in practice, since the statistics of an ergodic process may be empirically estimated from the sample statistics of a single realization of the process.
For the purpose of stochastic modeling, it is usually sufficient to consider only homogeneous and ergodic processes. Regional and non-ergodic variations of the process may then be effected by varying the model parameters or by simple postprocessing techniques rather than by incorporating these variations in the original model.
It is evident that (1) represents an infinite amount of
information
and consequently cannot be used in any realizable analysis or synthesis
procedure.
It is desirable to find a more limited set of statistics that
nevertheless define or perceptually differentiate a useful range of
phenomena.
A common simplification is to restrict consideration to
processes that can be adequately characterized by their second-order
statistics (n=2 in (1)), or by their moments, which serve
as ``expectations'' of the corresponding statistics:
An important class of stochastic processes in this respect are the Gaussian processes, whose nth-order statistics are jointly Gaussian, since the full statistics of a Gaussian process are uniquely determined by its first- and second- order moments.
Fortunately, these simplifications are not overly limiting. The restriction to second-order statistics has some basis in perception: the ``Julesz conjecture'' [14] asserts that random textures having identical first- and second-order statistics (differing in the higher-order statistics) cannot be visually discriminated. While counter-examples to the conjecture have been demonstrated, it is nevertheless regarded as being essentially accurate [33]. It seems likely that similar bounds may apply to the perceptual discrimination of statistical characteristics of (for example) terrains or fluid motion, but these have not been established to the author's knowledge.
Also, many natural processes are known or assumed to be Gaussian. The popularity of this distribution may be explained in part by the ``folk theorem'' that `a process that is a linear combination of many relatively uncorrelated effects will tend to be Gaussian.' This is a loose version of the central limit theorem, since a stationary linear filter is expressible as a weighted integral or sum of the input signal (c.f the discussion in [2], chapter 13).
It should be emphasized that non-Gaussian noises may be of interest,
and (with certain exceptions)
the second-order moments do not perceptually or otherwise determine
the noise in the non-Gaussian cases.
While stochastic texture synthesis using the full second-order statistics
is becoming computationally tractable with recent methods
[11,12],
it is expensive since it naively involves on the order
of
![]() joint probabilities if L is the number of gray levels
and N is the Markov neighborhood size or
``memory'' of the texture.
To date, most synthetic textures with controlled second- or higher-order
statistics have used a small number of gray levels (typically eight or fewer)
and joint probabilities defined over fairly small neighborhoods.
The textures produced under these restrictions
are often fairly abstract or artificial looking [32], and
published comparisons of textures
differing in the second-order statistics but having pairwise-identical
first- and second-order moments
have not clearly indicated the extent to which high-resolution stochastic
models may benefit from non-Gaussian statistics.
joint probabilities if L is the number of gray levels
and N is the Markov neighborhood size or
``memory'' of the texture.
To date, most synthetic textures with controlled second- or higher-order
statistics have used a small number of gray levels (typically eight or fewer)
and joint probabilities defined over fairly small neighborhoods.
The textures produced under these restrictions
are often fairly abstract or artificial looking [32], and
published comparisons of textures
differing in the second-order statistics but having pairwise-identical
first- and second-order moments
have not clearly indicated the extent to which high-resolution stochastic
models may benefit from non-Gaussian statistics.
Thus Gaussian processes are commonly adopted as a computationally tractable,
yet reasonably powerful, class of stochastic model.
The parameters of this model are
the first- and second-order
moments, that is, the mean
![]() ,
variance
,
variance
![]() ,
and the
autocorrelation function
,
and the
autocorrelation function
Intuitively, the autocorrelation function
describes the correlation between a random function and a copy
of itself shifted by some distance (``lag'').
For example, a completely uncorrelated or ``white'' noise has an
autocorrelation function
![]() (Dirac impulse function),
while a constant
signal is equally correlated with itself at all lags and so has
(Dirac impulse function),
while a constant
signal is equally correlated with itself at all lags and so has
![]() .
Usually the autocorrelation function decreases continuously away from the
origin, corresponding to a noise that is neither completely uncorrelated
nor deterministic.
The autocorrelation function of a noise with an oscillatory character
includes an oscillatory component that is damped away from the origin;
the period of this component corresponds to the average period of the
oscillation in the noise while the amount of damping is related to the
spectral bandwidth and the irregularity of the oscillation in the noise.
.
Usually the autocorrelation function decreases continuously away from the
origin, corresponding to a noise that is neither completely uncorrelated
nor deterministic.
The autocorrelation function of a noise with an oscillatory character
includes an oscillatory component that is damped away from the origin;
the period of this component corresponds to the average period of the
oscillation in the noise while the amount of damping is related to the
spectral bandwidth and the irregularity of the oscillation in the noise.
Stochastic modeling using Gaussian statistics and the second-order moments
may be termed spectral modeling since the noise
autocorrelation function and power
spectrum specify equivalent information, and in fact are a Fourier
transform pair (Wiener-Khinchine relation):
Experience in spectral modeling indicates that a wide and useful variety of phenomena may be described using this approach; some techniques and applications are surveyed in [2,1,27,41]. Spectral models have been used to generate reasonably good synthetic approximations of random textures such as sand, cork, etc. (e.g., [5]).
The analytic and computational techniques for spectral modeling
are also well established.
Fundamentally, a random processes is modeled as a white
noise with specified mean and variance input to a shaping filter h;
the problem is usually to define or identify h subject to
given empirical, analytical or computational restraints.
The power spectrum of the resulting process is simply
![]() where H is the Fourier transform of h.
where H is the Fourier transform of h.
For example,
fractal textures and terrains have been produced with a spectral modeling
approach using the spectrum f - d [43].
Other physically relevant spectra include the Markov
spectrum
![]() and the Lorentzian spectrum
and the Lorentzian spectrum
![]()
The spectral modeling approach encompasses these cases, as well as phenomena whose spectra are not as easily categorized.
The stochastic subdivision construction described by Fournier, Fussell, and Carpenter [10] will be generalized to synthesize a noise with prescribed autocorrelation and spectrum functions. It will be assumed that the reader is generally familiar with that work.
The basis of the Fournier et. al. construction is a midpoint estimation
problem:
given two samples of the noise, a new sample midway between
the two is estimated as the mean of the two samples, plus a random deviation
whose variance is the single noise parameter.
The construction is based on two properties of fractional Gaussian
noise:
1) When the values of the noise at two points are known,
the expected value of the noise midway between two known noise points
is the average of the two values.
2) The increments of fractional Gaussian noise are Gaussian,
with variance that depends on the lag and on the noise parameter.
Since only the immediately neighboring points are considered in
making the midpoint estimation, the noise autocorrelation information
is not used, and the constructed noise is Markovian.
This is not a limitation as long as the construction is used to model
Markovian noises, for example, a locally stationary approximation to Brownian motion.
However, the construction has been applied to the non-Markovian
fractional noises
![]() [9];
in these cases disregarding the required autocorrelation
produces ``creases'' (Section 4).
[9];
in these cases disregarding the required autocorrelation
produces ``creases'' (Section 4).
The general problem of estimating the value of a stochastic process given knowledge of the process at other points is one of the subjects of estimation theory and techniques such as Wiener and Kalman filtering [44,6]. There are several flavors of the estimation problem, depending on the available knowledge of the noise statistics, whether one is predicting, interpolating, or removing the noise, the estimation error metric, etc. The problem of stochastic synthesis is specifically similar to the application of digital Wiener prediction in the linear-predictive coding of speech (LPC) [34,18]: in both of these applications the values of a random process are estimated, and then perturbed and reused as ``observations'' in the subsequent estimation.
The discrete estimation problem for
a stationary one-dimensional random process
can be stated as follows:
Given observations or knowledge
of the values of a random process at times t + t k,
it is desired to form an estimate
![]() of the
process at time t, such that the expected mean-square error
of the
process at time t, such that the expected mean-square error
![]() is minimized for all values of the origin t.
This formulation appears to involve knowledge of the actual
values x (t) of the process
(in which case estimation would not be necessary), however,
the estimator is derived independently of the actual noise values
using only the noise autocorrelation function.
is minimized for all values of the origin t.
This formulation appears to involve knowledge of the actual
values x (t) of the process
(in which case estimation would not be necessary), however,
the estimator is derived independently of the actual noise values
using only the noise autocorrelation function.
A discrete stationary linear estimator has the form
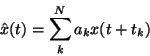
The geometric interpretation of the estimation problem in an abstract space of
random vectors is helpful [6,45].
In this interpretation, a random variable is treated
as an abstract vector, with the inner product of two vectors
x and
y defined as
![]() .
The estimation problem is then equivalent to the problem of
representing an arbitrary vector as closely as possible in the
subspace of ``observation vectors'' (known noise values).
The estimation error vector
.
The estimation problem is then equivalent to the problem of
representing an arbitrary vector as closely as possible in the
subspace of ``observation vectors'' (known noise values).
The estimation error vector
![]() is minimum when
s(t) is projected onto the subspace; in this case the error
vector is orthogonal to all of the observations.
is minimum when
s(t) is projected onto the subspace; in this case the error
vector is orthogonal to all of the observations.
In our case the midpoint
![]() at each stage in the construction will be estimated as a weighted sum of
the noise values x t known from the previous stages of the
construction, in some practical neighborhood of size 2 N
(Figure 1):
at each stage in the construction will be estimated as a weighted sum of
the noise values x t known from the previous stages of the
construction, in some practical neighborhood of size 2 N
(Figure 1):
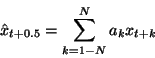
The estimated midpoint value
![]() will be displaced by an uncorrelated noise
u t + 0.5
of known variance to form a new noise point:
will be displaced by an uncorrelated noise
u t + 0.5
of known variance to form a new noise point:
The orthogonality principle then takes the form
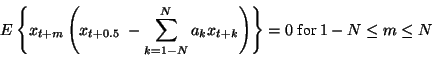
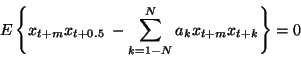
![\begin{displaymath}\setlength{\arraycolsep}{0mm}
\begin{array}{cccc}
\left[
...
...\\ {R( N -0.5)} \\
\end{array}
\right]
\par\\
\end{array}\end{displaymath}](img36.gif)
Since in stochastic subdivision the ``estimates'' are displaced and
then reused in the role of ``observation'' in the next subdivision stage,
it will be helpful to verify that the synthesized noise does in fact
preserve the specified autocorrelation function.
An expression for the autocorrelation function ![]() of the synthesized
noise is found by multiplying both sides of (3) by
x m and taking expected values, obtaining
of the synthesized
noise is found by multiplying both sides of (3) by
x m and taking expected values, obtaining
In general the coefficients will be different at different stages
in the subdivision.
The autocorrelation function R s of a scaled signal x(st)
is scaled by the same factor s,
Figure 2 shows the generalized subdivision technique applied to an nonfractal oscillatory noise. The implementation of the generalized subdivision technique is similar to the fractal subdivision technique; the only significant differences being the increased neighborhood size, ``boundary conditions'', and the need to solve (4) to obtain the coefficients a k for each subdivision level.
The matrix R ( m-k ) is symmetric and Toeplitz (all elements along each
diagonal are equal), permitting the use of efficient
algorithms available for the inversion of these matrices.
The efficiency of solving (4)
is probably not a major concern, however,
since the cost of determining and storing the coefficients for
a number of subdivision levels is small compared to the other
costs of synthesizing and viewing a high-resolution noise;
a standard Gaussian elimination routine was used here.
A simple test of the correctness of the coefficient solution procedure
is that the solution for the Markovian autocorrelation function
![]() should reduce to fractal subdivision,
that is, it should indicate nonzero coefficients only for the immediate
neighbors of the midpoint.
should reduce to fractal subdivision,
that is, it should indicate nonzero coefficients only for the immediate
neighbors of the midpoint.
The choice of the neighborhood size is of course a trade-off between accuracy of spectral modeling and efficiency. The vector space interpretation of the estimation problem confirms that the estimation error (7) will be reduced or remain the same as the neighborhood size increases, since increasing the neighborhood size is equivalent to increasing the dimension of the subspace.
An approach to determining the neighborhood size suggested in the estimation literature is to increase the size until the expected error variance (7) is reduced below a specified threshold. The Levinson recursion [15,22] is well suited to this approach. This algorithm solves estimation equations such as (4) recursively for each neighborhood size N given the solution for the previous size N - 1. The mean-square estimation error is also returned, so the recursion can be terminated when this error is sufficiently small. The Levinson algorithm would need to be modified for our purposes, since only even neighborhood sizes are used in stochastic subdivision.
Stochastic subdivision follows the general stochastic synthesis
scheme mentioned in Section 2, of shaping an uncorrelated noise
to produce the desired spectrum.
However, the estimator in stochastic subdivision is an
unusual ``filter'' because of its multiple-resolution capability
and because it is non-causal.
The Z-transform of (3)
(using an indexing scheme where the noise values from the previous
subdivision stage have odd indices, and the midpoint index is zero)
is
The cumulative spectral definition produced by the subdivision approach is greater than one would expect on the basis of the neighborhood size alone, however, since each stage in the subdivision models a limited part of the spectrum. This can be seen in Table 1, showing the coefficients for ten subdivision levels of an oscillatory Markovian (Lorentzian) noise. The coefficients for the first two (most global) levels are near zero, indicating that the noise is relatively uncorrelated at these scales. The coefficients for levels five and six have alternating signs, reflecting the oscillatory character of the noise, while the coefficients for the last two levels suggest that the noise assumes a Markovian character at small scales (as expected). It is concluded that large neighborhood sizes are probably not needed except where the scale of significant spectral features is smaller than an octave. Most of the figures in this paper were produced with a neighborhood size of four (or 4x4 in two dimensions).
It should be noted that the accuracy of the midpoint estimation can be improved by considering any known points from the current construction level (i.e. the midpoints of neighboring spans) as well as by increasing the neighborhood size over the points known from previous construction levels. These points were not considered in our derivation, however, because the order for computing the points at a particular subdivision level may not be known in advance. To impose an order on the computation would remove the non-causal advantage of the subdivision approach, while adjusting the estimation to utilize any encountered configuration of points would require different estimation coefficients for each such configuration and thus would complicate our explanation and implementation somewhat (although Eqs. (3), (4) are easily adapted for this purpose). It will be seen that high-quality noises result when only points from the previous construction stages are considered in the estimation procedure.
When the neighborhood size is greater than 2, the stochastic subdivision of a particular closed region will require reference to points outside the boundary of that region; this problem is analogous to the starting and boundary condition problems in some types of recursive filters and differential equation techniques.
The simplest approach to this problem is to assume periodic boundary conditions, so that a reference to a point s[t] outside the region [0..size-1] is mapped to the point s[p] using
p := t mod size; if (t < 0) then t := t + size;The noises produced with this approach are periodic, which is a useful property in some applications such as texture mapping.
A second approach is similar to the viewpoint-driven implementation of stochastic subdivision [4,10]. With this approach a region of noise can be subsequently extended by synthesizing the adjoining regions, which is not possible if periodic boundary conditions are used. The subdivision is seeded at the most global scale with given data, either obtained from a database or invented using uncorrelated random numbers. The displacement noise uses a spatially consistent random number generator as described in [4]. Then boundary points can be constructed as needed by subdivision from the neighboring seed points. If the required spatial extent of the synthesis is known at the outset, then at each subdivision level the required boundary points can be constructed, so these points will be available at the next level.
One numerical difficulty that has been encountered in practice
is that for certain autocorrelation functions
the determinant of the autocorrelation matrix R is zero at small scales
and (4) cannot be inverted.
In particular, this occurs for functions such as
the Gaussian
![]() or
modulated Gaussian
or
modulated Gaussian
![]() .
The Gaussian autocorrelation functions are effectively
positive semi-definite, since they correspond to
spectra that are (for numerical purposes) zero at more than
isolated points.
.
The Gaussian autocorrelation functions are effectively
positive semi-definite, since they correspond to
spectra that are (for numerical purposes) zero at more than
isolated points.
Random processes having positive semi-definite autocorrelation functions
are termed singular, as opposed to regular
processes, which have strictly positive definite autocorrelations.
A paradoxical result is that a singular random processes may be
predicted without error simply by Taylor series extrapolation,
given knowledge of its past or all of its derivatives at a point
[45].
Singular processes are sufficiently smooth at some scales that
some of the data are effectively colinear.
A useful spectral test for the existence of the derivative of a random
process is [45]
One approach to estimating a singular process is
to reduce the neighborhood
size until the rank of the autocorrelation matrix matches its
dimension and the matrix becomes positive definite.
It also should be possible to form a meaningful
though not unique estimate from the observations without
changing the neighborhood size.
Deutsch [6] recommends using a pseudo-inverse
rather than the inverse
of the autocorrelation matrix to obtain the estimation coefficients.
The author experimented with an iterative implementation of the
Moore-Penrose generalized inverse [6].
The generalized inverse of a nonsingular matrix is (numerically)
identical to the standard matrix inverse.
At scales where the determinant is numerically zero,
the generalized inverse sets the coefficients to
1 / 2 N ,
e.g.
![]() for N = 2.
The software should detect this and reset the coefficients to the
equivalent
for N = 2.
The software should detect this and reset the coefficients to the
equivalent
![]() in order to compute the displacement noise variance correctly.
in order to compute the displacement noise variance correctly.
Recalling that one of the primary motivations for stochastic models in computer graphics is to ``invent detail'', the two approaches favored here are simply to model the process over a range of scales such that it becomes smooth below or just above the pixel scale, or (better), to pick an autocorrelation function that generates detail at all scales. The small-scale behavior of the noise is governed by the behavior of the autocorrelation function near the origin (as we saw in the preceding remarks on the derivatives of random processes) or equivalently by the high-frequency portion of the spectrum. The considerations mentioned in this section should be kept in mind however, since any process whose spectrum falls off faster than f -1 will be numerically singular at small scales.
Haruyama and Barsky [13] have controlled the displacement noise variances in a stochastic subdivision procedure to obtain approximate spectral control of the noise. In some cases, however, changing the noise variances can produce artifacts. The ``creases'' sometimes encountered in stochastic subdivision can be related to the displacement noise variances and to the absence of autocorrelation information in Markovian subdivision. Each midpoint displacement divides a segment of the noise into two segments with different slopes. If the displacement variances are correctly chosen for a Markovian noise, the small scale subdivision displaces the noise from the slope trends established at larger scales, so that curvature of the fully interpolated noise is homogeneous. If the displacement noise variances fall off too quickly at small scales, however, the noise will tend to lie along the segments established earlier in the subdivision, and a large displacement at an early subdivision stage will produce a perceived average slope discontinuity or crease in the noise.
When the noise is not Markovian and the noise autocorrelation information is considered in making the midpoint estimate, the midpoint estimate will in general lie on a smooth curve passing through the nearby points from previous subdivision levels. Thus the subdivision avoids a ``slope trend'' and creases do not form as long as the variances are chosen with (7). The extent to which the variances can be altered from (7) is not completely understood, however. It was found experimentally that the variances could be altered to a considerable extent without producing artifacts. Haruyama and Barsky and Miller [25] also did not report any difficulties with creases using non-Markovian subdivision schemes. We hypothesize that creases do not form to the extent that the midpoint estimator acts as an interpolator. For example, the Markovian midpoint estimator is a linear interpolant and so can produce uncharacteristic discontinuities in slope when the variances are incorrectly chosen, while an estimator over a four-point neighborhood may result in uncharacteristic discontinuities in the second derivative when the variances are not chosen with (7).
The aliasing properties of stochastic subdivision are peculiar and relevant to the application of generalized subdivision. One of the main computational advantages of the subdivision approach is that different resolutions (at binary orders of magnitude) are available by varying the depth of the subdivision recursion, and so the resolution of the model can be locally minimized while maintaining a relatively constant image resolution.
The identification of stages in the subdivision construction with different resolutions is strictly incorrect however. This can be seen from one point of view by considering the problem of obtaining a half-resolution version of a given noise, for example, during an animation ``zoom-out'' sequence. A half-resolution noise that preserves the spectral content of the original noise up to the new, lower Nyquist rate is obtained by low-pass filtering to half of the original Nyquist rate and then dropping every other sample (``decimating'') [38]. From this viewpoint then the half-resolution noise produced in stochastic subdivision by reducing the construction level one step is obtained by decimating without any filtering. The low-pass filtered noise will not coincide with every other sample of the original noise unless it had no detail at frequencies above half of the original Nyquist rate. Thus, any spectral energy above half of the original Nyquist rate is aliased in the transition to the half-resolution noise.
Significantly, an aliased noise does not form coherent artifacts such as Moire patterns, rather, the noise at the lower resolution appears as a somewhat different noise than the original, so that the subject appears to ``bubble'' slightly during a zoom. The aliasing is limited for noises with monotonically decreasing spectra such as fractal noises, since the majority of the spectral energy remains unaliased in any resolution change. More serious anomalies can be expected if the subdivision recursion level is used to vary the resolution of a noise whose spectrum slope is flat or increasing at some scales, such as may be produced with the generalized subdivision technique. For example, the perceived noise in Figure 2 would change significantly between construction levels three and four if these were used as keyframes in a zoom.
A solution to this aliasing problem is required if the variable-resolution advantage of subdivision is to be achieved in generalized subdivision using certain spectra. One solution (suggested in [10]) is to keep the resolution of the last subdivision stages below the pixel scale, so that these effects are largely masked by the display resolution.
The main considerations for developing multi-dimensional generalized stochastic subdivision involve the specification of the subdivision topology and autocorrelation function in several dimensions. These considerations will be illustrated for the two-dimensional case.
 |
In multi-dimensional subdivision there may be several classes of points to
be estimated, categorized by their spatial relationship to the
points computed at previous subdivision levels
(this depends on the selected interpolation mesh).
For example, for the planar quadrilateral subdivision mesh shown in
Figure 3,
the midface vertex ``x''
will require different coefficients than the mid-edge
vertices ``o''
(the coefficients for each of the mid-edge vertices may be
identical aside from reflection or transposition,
depending upon the specified autocorrelation function).
Using our coordinate system with points from the previous subdivision levels
taking on integer indices, the midface and midedge vertex values will
be computed using
The coefficient matrix ar,c for each estimated
vertex can be obtained by solving
|
 |
Equations (9) and (10)
can be rewritten more generally as
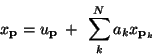 |
(11) |
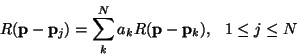 |
(12) |
 |
One practical difficulty in applying the quadrilateral subdivision mesh was encountered. With a large enough neighborhood, the coefficients of the outer observation points decay to insignificant values in an isotropic (or other) pattern. With a small neighborhood, however, the coefficients are truncated at the boundaries of the quadrilateral support. This introduces a non-isotropic bias into the construction: more correlation is introduced along the diagonal to the underlying mesh since the observation points are most separated at diagonally opposite corners on the quadrilateral.
This effect is often unnoticed (Figure 4), though it shows up when a long correlation noise is synthesized using a small neighborhood, or when such a noise is processed in some way. The diagonal bias can be eliminated by incrementing the neighborhood size until the outer coefficients are insignificant. If this is unappealing for efficiency reasons a more rotationally symmetric topology, such as an equilateral triangular mesh can be used. The author has employed a ``random quadrilateral'' subdivision scheme, in which several random neighborhoods are preselected using a non-biased random walk from the nearest neighbors of the point to be estimated, and one of these neighborhoods is chosen at random for each estimation.
In generalizing a one-dimensional autocorrelation or spectrum function to several dimensions, some care must be taken to insure that the autocorrelation function is nonnegative definite and corresponds to a nonnegative spectrum. The multi-dimensional autocorrelation and power spectrum must also be symmetric in several dimensions (e.g., R(y,x) = R( -y, -x)).
The most direct generalization of a one-dimensional function into
several dimensions is to a separable function,
that is, (in two dimensions)
f (x,y) = f x (x) f y (y).
Textures produced with separable functions have preferred directions
along the coordinate axes of the underlying sampling grid and may
be inappropriate where a naturalistic texture is desired.
A noise generated from a separable autocorrelation is not itself
separable, however, so the deterministic appearance of
truly separable textures is avoided.
The separable Markovian autocorrelation
![]() corresponds to a simple form of fractal quadrilateral subdivision
where the midface vertex is estimated only from the four vertices
defining the face (all other coefficients are zero regardless of the
neighborhood size), and the midedge vertices are estimated from the
two vertices defining each edge.
The coefficients for an isotropic Markovian noise are only slightly
different from this scheme (Table 2);
textures produced with the separable Markovian autocorrelation show
slight but noticeable directional tendencies.
corresponds to a simple form of fractal quadrilateral subdivision
where the midface vertex is estimated only from the four vertices
defining the face (all other coefficients are zero regardless of the
neighborhood size), and the midedge vertices are estimated from the
two vertices defining each edge.
The coefficients for an isotropic Markovian noise are only slightly
different from this scheme (Table 2);
textures produced with the separable Markovian autocorrelation show
slight but noticeable directional tendencies.
The autocorrelation and spectrum of an isotropic noise are radially
swept profiles:
![]() .
Unlike the separable case, the one-dimensional functions defining
n-dimensional isotropic autocorrelations and spectra
do not form a Fourier transform pair, but rather can be expressed
as a Hankel (or Fourier-Bessel) transform pair [2]
.
Unlike the separable case, the one-dimensional functions defining
n-dimensional isotropic autocorrelations and spectra
do not form a Fourier transform pair, but rather can be expressed
as a Hankel (or Fourier-Bessel) transform pair [2]
| (13) |
In addition to the general requirement of a nonnegative definite
autocorrelation, several specific constraints have been reported
for multi-dimensional isotropic autocorrelations and spectra:
The spectrum of a three-dimensional isotropic noise must be monotonically
decreasing (so three-dimensional isotropic noises cannot be oscillatory),
and a minimum bound on the normalized
autocorrelation function for an n-dimensional
isotropic noise is - 1 / n [41].
A rather complicated expression for the n-dimensional isotropic
correlation produced by a swept one-dimensional C 1 profile is given
in [23]; for two dimensions it reduces to
| (14) |
A function
![]() ,
which violates the minimum bound constraint, was tried in the subdivision
procedure.
The solution yielded negative determinants at some subdivision levels,
confirming that this function is not positive definite.
The computed midpoint displacement noise variances were also negative
at these levels.
,
which violates the minimum bound constraint, was tried in the subdivision
procedure.
The solution yielded negative determinants at some subdivision levels,
confirming that this function is not positive definite.
The computed midpoint displacement noise variances were also negative
at these levels.
Probably the most interesting noises are those that are neither separable nor isotropic, but that have an intrinsic directional structure. Non-isotropic autocorrelations can be produced, for example, by stretching or modulating an isotropic autocorrelation. Unless the constraints on the autocorrelation function are well understood however, it may be easier to manipulate the power spectrum to a non-isotropic form (insuring that it remains non-negative) and obtain the autocorrelation using the Wiener-Khinchine relation (2).
The autocorrelation function can also be numerically estimated
from a digitized texture
p [ r , c ] using
![\begin{displaymath}R ( y , x )
=
\frac{1}{ N ^ 2 }
\sum _ {r=0} ^ N \sum _ {c=0} ^ N
p [ r , c ] p [ r + y , c + x ]
\end{displaymath}](img81.gif) |
(15) |
The generalized subdivision technique extends the subdivision approach
to produce artifact-free noises with a variety of spectra.
Figure 4
show several textures produced using the generalized
subdivision technique.
Figure 5 illustrates the external consistency property
of stochastic subdivision techniques.
In this figure a height field is synthesized using the luminance from
a well known image (averaged down to 32 2 pixels) as seed data.
In Figures 6a-d
the gray levels in several synthesized textures are interpreted as
heights to produce several distinct types of synthetic terrain.
The height values in some figures were modified by a power law,
for example in Figure 6a the heights y were modified by
![]() .
This has the effect of making the noise nonstationary by
selectively exaggerating the most prominent features of the noise.
Power modification also alters the distribution and local spectrum of the
noise and so should
be used with care when a particular distribution and spectrum are required
for theoretical reasons. The use of this technique its effects on the
spectrum are briefly described in [16].
.
This has the effect of making the noise nonstationary by
selectively exaggerating the most prominent features of the noise.
Power modification also alters the distribution and local spectrum of the
noise and so should
be used with care when a particular distribution and spectrum are required
for theoretical reasons. The use of this technique its effects on the
spectrum are briefly described in [16].
The disadvantages of the generalized subdivision technique include the increased computational cost of considering larger neighborhoods in the estimation procedure, and the need to determine or invent the autocorrelation or power spectrum function of the desired noise. The latter is perhaps the most important issue in applying this technique. The obvious approaches to this issue are to empirically determine the autocorrelation or spectrum of the prototype phenomenon or to select these functions on theoretical grounds (in computer graphics we add the third possibility of ``trying things until it looks right'').
Although it has been suggested that the fractal spectrum f - d is to be preferred for theoretical reasons over other spectra for modeling many natural phenomena, theoretical and empirical arguments for considering other types of spectra will be mentioned.
Several researchers have concluded that the f - d spectrum
(or equivalently the ``fractal dimension'') is not adequate to
describe natural phenomena of interest over all scales [24,29].
Empirical studies of the possible fractal nature of various phenomena
have also found that the fractal dimension is often different at different
scales, although ranges of scales described by a constant dimension were
found [21,3].
In fact there is a relation between the fractal dimension D and the
exponent d in the fractal power spectrum f - d [43]
| (16) |
These arguments do not deny that the assumption of a power-law spectrum is a convenient analytical simplification. If ``fractal analysis'' is to be more than a procedure of fitting straight line segments through a spectrum curve plotted on log-log axes, however, it should be established that the attributed power law is accurate over an unexpectedly broad frequency interval, or that there are theoretical reasons for expecting this spectrum. The often-cited fractal interpretation of Richardson's coastline data has been questioned on these grounds because the data describe a fairly limited range of scales (less than two orders of magnitude in all but one case) and because there is no reason to expect the processes involved in very large scale (continent formation) and small scale coastline formation (e.g. erosion) to have similar statistics [37,39]. It also appears that the nominal 1/f noises in electrical circuits may only approximate fractal behavior [26]).
Theoretical models predicting the fractal spectrum have not been forthcoming in most cases (an exception is the well established Kolmogorov - 5/3 law in the statistical theory of turbulence [27]). In fact, the f - d spectrum is a priori an unlikely choice for a theoretical model, since the integral of this function diverges, and consequently a phenomenon that strictly obeys this spectrum is nondifferentiable and has infinite characteristics (length, average power). The viability of this aspect of the fractal model was also questioned in the geophysical literature [19,39].
Although some fractal practitioners state that the fractal model is only
intended to apply over a limited range of scales,
the global properties of self-similarity and non-differentiability are
the distinguishing features of the fractal model.
If these features are not required,
one could adopt other spectra that fall off according to a power law
over the desired range of scales.
For example, the Markov-like spectra
![]() are commonly used as a ``first-order fit'' for many phenomena;
these spectra are similar to the fractal spectrum
at high frequencies
yet do not diverge at low frequencies
(the Markovian spectrum (d = 2) has a physical basis, e.g., in
Langevin's equation for Brownian motion [45]).
are commonly used as a ``first-order fit'' for many phenomena;
these spectra are similar to the fractal spectrum
at high frequencies
yet do not diverge at low frequencies
(the Markovian spectrum (d = 2) has a physical basis, e.g., in
Langevin's equation for Brownian motion [45]).
One advantage of the fractal model over many others is that it generates
detail at all scales. The general spectral
modeling approach advocated here can also generate detail at all scales,
without sacrificing differentiability and scale-dependent features.
The nondifferentiability of the fractal models results in terrains that
in the author's opinion appear too rough at
small scales (e.g., Figure 7 and [42]).
Most of the terrain figures accompanying this article
were produced using two-dimensional variations of a ``Markaussian''
autocorrelation
![]() with
with
![]() ,
which produces noises falling between the extremes of the Gaussian (too
smooth) and Markovian (usually too rough) textures shown
in Figure 4.
,
which produces noises falling between the extremes of the Gaussian (too
smooth) and Markovian (usually too rough) textures shown
in Figure 4.
The desirability of scale-dependent features for visual modeling is also obvious: most visual phenomena provide at least an approximate sense of scale (atmospheric phenomena are perhaps the exception again). As an illustration, one would be surprised to find a terrain such as Figure 6a at one's feet, and the scale-dependent depressions in Figure 6c certainly do not detract from the realism of that terrain. The lack of scale-dependent features can be a practical problem in visual terrain simulation, since without such detail the observer cannot judge the distance to the ``ground''.
We conclude that, although a single descriptor such as the fractal dimension or spectrum exponent may be adequate for some classification purposes, the validity of the fractal model is not well established for many natural phenomena, and it is evident that the visual characteristics of many phenomena cannot be adequately differentiated using only this model. For example, it was found in [3] that an airport runway had a fractal dimension identical to that of some topographical data, the interpretation being that this was due to the attenuated low-frequency variation of the runway.
Spectral modeling with Gaussian processes permits the description of a variety of phenomena, including fractal noises as a special case. Important perceptual characteristics of the noise, such as scale, period of oscillation, and directional tendencies are directly reflected in the noise autocorrelation function. Other characteristics such as dominant scales of detail and the small-scale or high-frequency behavior of the noise are easier to specify in the frequency domain, using the intuitive interpretation of the spectrum as the amount of detail at each scale.
The criteria for evaluating the suitability of a stochastic synthesis method for computer graphics applications include efficiency, quality of the synthesized noise, and the degree of control over perceptually observable characteristics of the noise. Due to the very large size of the synthesized databases used in a complex image or an animation, the efficiency criterion often becomes a concern for practicality. Local methods that permit independent synthesis of portions of a large database are preferred over global methods in which the whole database is generated in one step.
A brief comparison of some stochastic synthesis methods will be given below in order to further characterize the method presented here. With this purpose in mind it will be assumed that the reader is acquainted with several of these methods, and the comparison will be restricted to the previously mentioned criteria.
Fourier (FFT) synthesis [43]. This method is global. It has the advantages of simplicity and efficiency (for a global method); it also provides exact spectral control.
Stochastic subdivision [10]. This method is local. It produces an approximate f - d noise, and an exact Brownian noise for d = 2. `Crease' artifacts are usually visible for d > 2. Stochastic subdivision is unique in its capability of refining an existing database. A variation of stochastic subdivision [13] allows the noise variances to take on arbitrary values across subdivision levels, thus approximating a wider range of spectra (oscillatory noises are not possible however). Another variation [25] uses a higher quality interpolant for the point estimation, alleviating the problem with creases.
Fractional Brownian simulation [8]. This method applies a standard multivariate simulation technique in which uncorrelated random variables are linearly transformed by a factored form (Choleski decomposition) of the desired correlation matrix. The method is global and less efficient than FFT synthesis (it is O( N 2 )), though an incremental refinement method that is local in a limited-precision implementation is described.
Poisson faulting process [20]. The Poisson faulting process is a sum of randomly placed step functions with random heights. It produces a Brownian noise (f -2 spectrum). A related technique is sparse convolution [16,17], in which an arbitrary function is convolved with a Poisson point process (in one dimension the Poisson faulting process is a special case of sparse convolution). The resulting spectrum is the transform of the (deterministic) autocorrelation of the function. These methods can be implemented locally [16] using an internally consistent approximate implementation of the Poisson process. They are equivalent in efficiency to convolution. The superposition of the function may be visible in the synthesized noise if the Poisson process is too sparse.
Interpolated noise lattice [30,31]. In this method an uncorrelated noise defined on a lattice is interpolated to generate an approximately bandlimited noise. This is employed as a spectral basis, with a desired spectrum being approximated as a weighted sum of these noises at different scales. The noise lattice is internally consistent, so the method allows local synthesis. With a standard interpolation method the interpolated noise does not provide an ideal spectral basis, since the low frequency power in the noise lattice is not removed and cannot be removed in summation (subtracting power spectra is not meaningful). In several dimensions standard (tensor product) interpolation schemes also result in preferred directions along the lattice axes. A variation of the interpolated noise lattice method [17] substitutes Wiener interpolation, which provides greater spectral control (with some restrictions) and eliminates the spectral summation.
Generalized stochastic subdivision. The technique presented here is best described as semi-local. It can approximate an arbitrary spectrum to a desired degree of accuracy, and the accuracy of spectral modeling can be traded for efficiency. The required neighborhood size depends on features of the desired spectrum (e.g., the number of maxima) and on the desired accuracy of the spectral modeling. In common with the other subdivision techniques, it allows incremental synthesis and refinement of an existing database. The implementation is somewhat more complex than that of most of the other methods.
<733>>**COMMENT
The generalized subdivision technique has not been fully explored. The case of non-functional noises described in [10] (produced using vector displacement of the midpoints in the direction perpendicular to the local normal) was not considered. Future work also includes further exploration of the constraints on the autocorrelation function. COMMENT
| E | Expectation |
| R | Autocorrelation function (autocovariance function) |
| S | Power spectrum |
| x t | Noise value |
| u t | Uncorrelated displacement noise |
| a k | Estimation filter coefficients |
| N | Neighborhood size |
Elassal, A., and Caruso, V. Digital Elevation Models. National Cartographic Information Center, Reston, Va., 1984.
Received January 1986, accepted January 1987