J. P. Lewis
Computer Graphics Laboratory
New York Institute of Technology
Creation by Refinement (CBR) is a neural network `creativity' paradigm which can create novel examples of a learned class of patterns. In theory, CBR solves the analysis-resynthesis problem: CBR can generate synthetic forms which mimic arbitrary prototypes. In practice, this universality is tempered by the current absence of known bounds on the network training time and size required to learn particular problems. Nevertheless there is some consensus that neural networks may provide natural (and thus relatively efficient) representations of phenomena such as texture which are characterized by a `fuzzy' structure. We consider the potential application of CBR to the problem of generating irregular shapes and textures, and show some preliminary experiments in this direction.
La Création par Raffinement (CBR) est un paradigme connexionniste du pouvoir créateur capable de produire des exemples nouveaux et originaux d'une classe de dessins. Théoretiquement, CBR résoud le problème de l'analyse et de la synthèse. En actualité, cette universalité est rédouit par l'absence des limites connues sur le temps et le dimension nécessaire pour qu'un modèle connexionniste apprenne des problèmes particuliers. Toutefois, il y'a de la concordance qu'un modèle connexionniste pourrait produire des représentations naturelles et ainsi efficaces des phénomènes, comme les textures caractérisés par des structures ``vagues''. Nous considérons içi l'application potentiel de la CBR au problème d'engendrer des textures et des formes irregulières et nous présentons quelques expériences préliminaires dans cette direction.
Keywords: Pattern, Shape, Texture, Neural Network, Connectionism.
Connectionist or neural network approaches have several proposed advantages over standard algorithmic approaches, including the promise of computation without programming and the ability to represent ``fuzzy'' structure. These advantages are potentially relevant to applications including visual simulation and computer arts which require the generation of novel patterns having a desired structure.
We will consider the potential application of a recently introduced neural network pattern creation paradigm to image synthesis problems. This paradigm, termed Creation by Refinement (CBR), has the capability of creating novel samples from a class of patterns that is specified by example rather than by rule. Such a capability, if realizable, would have practical value for simulating phenomena for which the formulation of an algorithmic description is difficult or inconvenient, and for which general techniques such as probabilistic modeling are inadequate. Difficult modeling or rendering problems might be solved by gathering photographs or measurements of sample objects, rather than by developing specific algorithms.
Non-connectionist approaches have not provided a complete solution to the problem of describing and generating irregular forms. In order to characterize the potential of CBR for this purpose, we will first briefly describe several other general approaches.
In a model-based approach, a surface form is considered as the result of an underlying model, which is implemented as an algorithm. If a correct model can be identified and implemented, this approach will obviously generate good results. It requires the identification and implementation of a model for each desired class of pattern.
In a more general structural approach, a rule-based system such as a picture grammar having no particular claim to being a correct model is fit to the desired class of patterns (e.g. [1]).
In common probabilistic approaches, a class of patterns is represented by their joint nth-order probability distributions, and new forms can be created by sampling from this distribution. The full probability distribution function is an impractical amount of information however. Only restricted subsets of the probabilistic model have been employed in practice, for example, spectral synthesis methods and fractals which use only the second-order moments of the full joint probability distribution.
The second-order moment (equivalently, power spectrum and autocorrelation) descriptions have been the basis for most texturing algorithms in computer graphics [2,3,4,5]. While it has been argued that the the second-order moments describe a considerable range of natural textures, it is also well known that these statistics do not capture the full range of perceptible structure [5]. For example, the second-order moments are invariant with respect to reflections of both the domain axes and the dependent variable, and thus asymmetry with respect to either the independent or dependent variables cannot be described. The height profile of a field of pebbles could not be synthesized by a second-order moment approach (Fig. 2).
Interesting irregular forms may contain considerable structure despite their irregularity. Capturing structure by purely probabilistic modeling is inefficient, and capturing additional structure by adding higher-order statistics gives (explosively) diminishing returns. To illustrate these remarks, consider the statement tree branches are narrower than tree trunks. The description of the widths of branches and trunks via a probability distribution requires representing the entire space of ``width events'' in which the branches are larger than the trunks, simply to assert that the probabilities of points in this space are (near) zero. In contrast, the information in this statement could be represented much more compactly as a rule. On the other hand, a description by rule would not naturally describe the distribution of trunk and branch width variations.
A wide variety of different models are presently grouped under the ``neural net'' label. While some of these models are biologically inspired, many models might be better labeled as adaptive or distributed pattern recognition schemes. The computational properties of these schemes are of interest independent of their biological relevance.
The perceptron family of neural nets performs supervised classification of patterns. That is, a perceptron-like net is trained to associate input patterns with desired corresponding output patterns (classifications). The training occurs by repeatedly presenting the associated pairs of patterns to the network. These nets can also generalize (correctly classify previously unseen patterns) in some cases.
Perceptron-like nets consist of notional neurons arranged in one or more layers. Each neuron computes an inner product of an input pattern with its weight vector (``synapses''). The training process changes these weights. The inner product is then passed through a nonlinearity (such as a threshold in the case of the classic perceptron model [6]). The neuron is therefore computing where the input pattern lies with respect to the hyperplane represented by its weights; this can be considered as computing one ``feature''.
A major development in the theory of perceptron-like networks was the identification of an algorithm to train a network consisting of more than one layer of neurons, with the output of each layer serving as the input pattern for the next layer. This back propagation algorithm is described in [7] and other sources. It is essentially a extensive application of the chain rule, where the partial derivatives of the error between an obtained output pattern and the desired pattern are taken with respect to all the weights in the network. At each presentation of a pattern pair, the weights are moved a short distance in the error minimizing direction, performing a gradient descent search in the weight space.
The back propagation algorithm inspired the development of a variety of other multi-layer neural networks. Some of the characteristics of back propagation and similar networks will be summarized in the following paragraphs.
It is known that suitably constructed multi-layer networks using a nonlinear activation rule can represent arbitrary mappings (functions) [8]. Such networks can thus in theory represent arbitrary pattern recognition tasks.
It has also been demonstrated that supervised gradient descent learning (SGDL) nets such as back propagation can deduce various smooth maps given a sufficient number of sample points in the domain and range of the map. Much current experimentation and thinking addresses the question of whether this learning capability is general, robust, and interesting.
SGDL nets may find local rather than global minima. Neural net folklore asserts that local minima may not be as much of a problem as in other gradient descent optimization techniques for reasons relating to the very high dimensionality of the search space.
At present there are few known bounds on the number of training
patterns [9] and neurons,
and the amount of computation required for SGDL nets to
learn particular problems.
This fact, combined with the computational expense of current SGDL algorithms
(which is sometimes measured in days on conventional
MFLOPs computers)
means that the promise of computation without programming is somewhat
hollow. While networks to solve apparently arbitrary
recognition problems exist in theory,
there is no guarantee that the required net for a particular problem
can be found
in less time than it would take to derive an algorithm for the same problem.
Neurons within a given layer may compute in parallel. Neural nets sometimes form distributed representations, in which particular neurons can be removed without significantly changing the overall network response (fault tolerance).
There are a number of experiments and considerable enthusiasm to the effect that neural networks including SGDL nets are effective for certain perception-like problems that are characterized by the combination of structure and irregularity. It has been suggested that algorithms such as back propagation are in fact capable of discovering required high-order statistical constraints without wasting computation on high-order statistics which are not characteristic.
SGDL nets require a differentiable nonlinearity. A sigmoid (S-shaped) nonlinearity is commonly used. Depending on the magnitude of the argument to this nonlinearity, it may serve as a nearly linear transfer function (small arguments), or as a nearly threshold nonlinearity (large arguments). With threshold-like nonlinearities, multi-layer nets can compute Boolean functions. Thus, individual neurons can compute ``fuzzy'' or algorithmic decisions as needed. This characteristic supports the previous comment about the suitability of neural networks for perception-like problems.
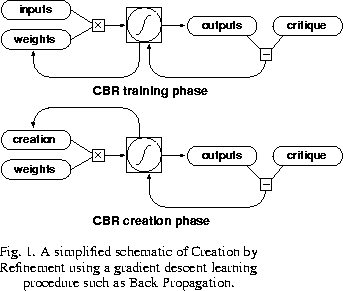
The gradient descent version of Creation by Refinement consists of a training phase, in which a standard (e.g. SGDL) network learns to identify patterns of a desired class, followed by a creation phase, in which a random `creation' is refined by a gradient descent search complementary to the one used in training (Fig. 1).
More specifically, the network is to learn a critique function (mapping)
where
![$i \in [0,1]^m, o \in [0,1]^n$](img5.gif){kind=small}
and typically 
.
For a texture synthesis application, i might be an array of color values,
and o might be simply a corresponding critique bit indicating whether
i is in fact a suitable example of a desired class of texture.
The training proceeds as follows:
.
is obtained.
and the corresponding desired output
(critique)
is used as an error signal to adjust the
network parameters wk in the direction
.
has hopefully converged to the
desired critique function 
.
Following successful training of this ``critic'' network, the (pseudo)inverse of the learned critique function is probabilistically explored to generate new patterns. Specifically,
.
,
that is, c satisfies the
desired critique.
CBR is described in more detail in [13,18].
CBR is termed a `paradigm' since it does
not specify a specific critic algorithm, but rather
specifies a way of making use of any suitable critic net.
In this respect it is similar to paradigms for employing
SGDL nets for function optimization [10]
and data compression.
CBR is applicable using any supervised gradient descent
learning network because
knowledge of the error gradient with respect to the weights
entails being able to calculate this gradient with respect to
the inputs: inputs may be considered as weights
on `virtual inputs' having a unit value.
In the back propagation algorithm [7],
the error gradient with respect to the inputs is
available following the back propagation pass.
Using the notation in [7], this is:
is the back-propagated error component,
c m is a component of the creation input,
and the summation is over units
receiving input from cm.
More generally, CBR as described above may be employed with any feedforward pattern association network having a differentiable nonlinearity at the neuron. A CBR-like procedure for competitive learning nets (which need not have differentiable nonlinearities) has also been introduced [11], and CBR-like adaptations of certain non-connectionist pattern recognition techniques are currently being considered.
In order for there to be more than one creation,
the critique function learned in training must be many-to-one.
In fact the preimage of a particular critique is potentially quite large.
In the standard neuron architecture,
the space of equivalent inputs accepted by a particular
network unit satisfies
for a given constant k.
This space is a hyperplane of dimension n - 1 for a unit with n inputs.
Similarly holding constant the outputs of all other units
with these same inputs
reduces the equivalent input space to an intersection of hyperplanes
or affine set of typically much lower dimension, but
the arbitrarily fixed outputs represent only one point in a
hyperplane of inputs accepted by a subsequent network layer.
The preimage of a particular critique must also be limited to acceptable creations. This requires that the initial training set adequately sample the input space; it must include nonsensical as well as useful examples. For example, if a network is trained on a Boolean relation, what will the net output if an analog-valued input is presented? The preimage of a Boolean output value may not be restricted to `legal' Boolean inputs. If CBR is invoked on such a network, non-Boolean creations such as 0.5,0.5 can result.
Analog input values can be disassociated from Boolean output values
by including additional relations such as
in the training set.
Since in general we do not know how to construct a training set which
adequately samples the creation space,
the CBR procedure is amended to include
the possibility of adding any undesirable creations to the training
set and retraining.
This is termed restricting the domain.
Training SGDL nets is quite difficult. If a particular network has not yet succeeded in learning a given problem, it may be that the network is too small (or too large) for the particular problem, or the training set may be inadequate, or it may be that more time is required. This uncertainty means that considerable patience is required, particularly since the training may require hours or days. The creation phase of CBR is usually quite rapid in comparison to the training phase because networks are chosen to have many more weights than inputs for most problems.
Neural net experimentation requires a flexible software system. We developed built-in vector operations for several Lisp systems. This provided nearly the efficiency of a compiled language (since most of the computation in neural nets can be vectorized) as well as the convenience of a high-level and interactive programming environment. For example, this approach allowed experiment scripts to contain procedures for generating new training patterns `on the fly'.
Fig. 3 shows ``Doodles'' generated using a variation of CBR. In this variation, a minimal training set is defined initially. This training set need not sample many areas of the desired function. The training phase is then repeatedly interrupted and the creation phase is invoked. The resulting random creations are critiqued and added to the training set. In this way, the training set is built incrementally during the training.
This procedure is termed reinforcement CBR since it seemingly converts a SGDL algorithm into a reinforcement learning algorithm (e.g. [12]; reinforcement CBR is described more fully in [13]). In reinforcement CBR the net effectively has a critique of its current internal representation, and so it can be guided away from forming undesired representations such as memorization of the training patterns. This has been found to accelerate learning in some experiments.
As in many other neural network demonstrations, some of the
structure evident in Fig. 3 is due to the selection of
an appropriate representation space for the learning problem.
In Fig. 3, the network input units represent the curvature
of the doodle parameterized by the curve length s.
The curve is then constructed by
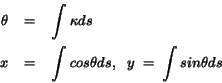
We have found that SGDL nets train reliably and fairly quickly on simple problems whose solution is known. For example, back propagation quickly learns to be a linear filter when the training data are generated by an existing (algorithmic) filter. One reason why training may be more successful when the solution is known is that in this case training pairs can be synthesized as needed; training cannot fail for reason of too few training pairs. While we have implemented texture synthesis by training the critic net to filter random inputs (mainly to confirm that various net algorithms were functioning), results will not be presented since there is little practical value to a neural net which mimics existing algorithms.
Fig. 4 is one of the few results we have obtained which does not appear to mimic an existing filter (although this pattern might be obtainable with a reaction-diffusion model). In this experiment, the training patterns contained a single randomly placed circle on a 642 field. Counterexamples were generated by the reinforcement CBR procedure. The input was preprocessed by a feature detection layer (see the following section) which performed a correlation (inner product) of the circle prototype including some surrounding field with the input field at each location in a 162 subsampled window. The network's learning task was then to learn a Boolean OR-like function. The cascade correlation learning algorithm [14] was used. Input values were coded as -1,1 rather than the usual 0,1.
Many researchers are developing alternative learning algorithms that address the practical limitations of back propagation. We experimented with one alternative algorithm, cascade correlation [14]. This algorithm incrementally adds neurons as needed to solve a particular problem, and thus it eliminates the need to guess the required network size. The results obtained so far with this algorithm have been mixed.
Although SGDL nets can in theory perform both feature discovery and pattern classification, it has been proposed that they only perform well on the latter task [15,16]. It has also been observed that many difficult learning problems can be transformed into simple learning problems by appropriate predetermined transformations of the problem space. There are several new and more promising learning algorithms which perform feature extraction or simplifying transforms on the problem space before classification, or which (sometimes equivalently) adopt faster converging basis functions (back propagation can be viewed as approximation by sigmoid basis functions). We hope to identify or develop a hybrid feature-detection/classification network suitable for shape description.
It is evident that the capabilities of CBR depend largely on the capabilities of the underlying critic network. The practical value of CBR (and many other neural net approaches) is remarkably difficult to evaluate at present.
On the positive side, as mentioned above, suitable multi-layer SGDL networks can represent arbitrary recognition functions. Thus, we can in concept consider fantastic applications of CBR, such learning to recognize great paintings, and then producing new masterpieces. (Of course, this may be an impossible learning task if in fact great paintings are designated by factors other than their visual characteristics).
Pragmatically, the scaling properties of many neural net algorithms are poorly understood, and in general there are no known bounds on the computation required for particular tasks.
Very few theoretical results are available for nonlinear neural nets, and the field is driven largely by experimentation. Unfortunately there is little consensus or basis for evaluating the results of most neural net experiments.
In practice, the results obtained with CBR to date are unimpressive. In defense of this work, however, we remind the reader of an important rendering technique which was introduced with fairly unimpressive images [17]. Also, some models (e.g. Turing machines) have conceptual value despite their limited practicality.
We feel that CBR has some conceptual value as a holistic paradigm for pattern creation. CBR appears to be more suitable for computer arts applications such as the machine composition of music than other current approaches [13,18]. It also has some general resemblance to artistic creativity: students of art and music composition are often first taught to become critics, i.e., to recognize the features of good art. When students are experiencing difficulty in composing their first works, some teachers will urge the students to `put down anything, see what it suggests, and refine it'.